# （必須）モジュールのインポート
import os
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt

# 表示設定
np.set_printoptions(suppress=True, precision=3)
%precision 3

'%.3f'

3. NumPyの基礎

本章は以下の文献とウェブサイトを参考にしています：

• Wes McKinney, Pythonによるデータ分析入門，オライリー，2018

• Jake VanderPlas, Pythonデータサイエンスハンドブック，オライリー，2018

• note.nkmk.me: https://note.nkmk.me

3.1. Numpyとは？

3.1.1. NumPyとは？

スポーツのデータセットは画像，ドキュメント，座標，など様々なフォーマットを持つが，これらは数値や文字列を格納した配列として扱うことができる．例えば，試合を撮影した動画はフレーム単位ではデジタル画像として表されている．デジタル画像は2次元配列として表され，配列の各要素が各ピクセルの輝度（RGB値）に対応している．また，選手の位置座標は \((x, y, z)\) の時系列データとなっているので，各座標成分の時系列データとして扱えば，2次元配列として表すことができる．

このように，データ分析では，数値や文字列を効率的に格納することが必要となる．Pythonには，配列を扱うためのリストという機能が標準搭載されているが，サイズの大きいデータを扱うのには不向きである．そこで，大規模な配列を高速に処理するためのライブラリとしてNumPy（ナンパイ）が用意されている．NumPyの配列はPythonの組み込みリストと似ているが，配列のサイズが大きくなるにつれて，より効率的なデータ操作ができるように設計されている．

3.1.2. NumPyのimport

NumPyはnpという名前で以下のようにimportするのが慣例である：

import numpy as np

これにより，NumPyの関数（例えばfunc関数）を使うときにはnp.func()のように実行できる．

3.1.3. Numpy配列とリストの違い

リスト

Pythonのリストは以下のように整数と文字列など複数の型を同時に格納することができ，多次元にすることも可能である． また，行ごとに異なるサイズにすることもできる．

[[1, 'a', 10.0], [2, 'b']]

[[1, 'a', 10.000], [2, 'b']]

NumPy配列

NumPy配列を生成する方法は後ほど詳しく説明するが，np.array関数を用いて組み込みリストを変換するのが基本である．

np.array([[1, 2], [3, 4]])

array([[1, 2],
       [3, 4]])

NumPy配列は組み込みリストと同様に多次元配列を実現できるが，全ての要素が同じ型を持ち，各行のサイズも同じでなければならないという制約がある（データ型をobjectにすれば実現できなくもないが，これは用いるべきではない）． 一見するとPythonの組み込みリストの方が使い勝手が良いように見えるが，Numpy配列には以下のような長所があるため，特に大規模な数値データを扱う際に威力を発揮する．

1. リストに比べて高速に動作する

Numpyの内部はC言語によって実装されているため，特に大規模なデータを扱う際にリストとの違いが顕著になる． 以下は0から9999まで1ずつ増える配列をリストとNumpy配列で生成する例である．

※マジックコマンド%%timeを使用することで，セル全体のコードの実行時間を測定することができる．

%%time
x_list = []
for i in range(10000):
    x_list.append(i)
print(np.array(x_list))

[   0    1    2 ... 9997 9998 9999]
CPU times: user 947 µs, sys: 56 µs, total: 1 ms
Wall time: 969 µs

%%time
x_numpy = np.arange(10000)
print(x_numpy)

[   0    1    2 ... 9997 9998 9999]
CPU times: user 201 µs, sys: 32 µs, total: 233 µs
Wall time: 208 µs

2. 配列全体に対する高速な演算が可能でコードがシンプル

この機能はユニバーサル関数と呼ばれ，配列に対して演算を行うだけでそれが各要素に適用されるのでコードがシンプルになる． リストで同じ結果を得るためにはfor文を使う必要があるが，pythonではループ処理が非常に遅くかつコードが煩雑になる． 以下は，配列の各要素を2倍するコードをリストとNumpy配列で実装した例である．

%%time
for i in range(len(x_list)):
    x_list[i] = x_list[i] * 2
print(np.array(x_list))

[    0     2     4 ... 19994 19996 19998]
CPU times: user 1.42 ms, sys: 46 µs, total: 1.47 ms
Wall time: 1.46 ms

%%time
x_numpy = x_numpy * 2
print(x_numpy)

[    0     2     4 ... 19994 19996 19998]
CPU times: user 212 µs, sys: 54 µs, total: 266 µs
Wall time: 236 µs

3. 高速に動作する関数やメソッドが利用可能

例えば配列をソートしたいとき，NumPyや類似のパッケージを使わない場合は自分でソート関数を作る必要があるが，それがエラーなく高速に動く保証はない． 一方，NumPyには予めnp.sort関数が用意されているためこれを用いるだけで済み，さらにアルゴリズムを選択することもできる．

# 0~10までの整数をランダムに生成して，ソートする
a = np.random.randint(0, 100, 10)
np.sort(a)

array([ 2, 14, 48, 48, 62, 65, 68, 68, 72, 98])

3.1.4. NumPy配列のデータ型

np.array関数でデータ型を明示的に指定したい場合にはdtypeキーワードを用いる．dtypeで指定できる主要なデータ型は以下の通りである：

• int（整数）

• float（浮動小数点数）

• bool（真偽値：True／False）

より詳しくfloat64のようにビット長を指定することもできるが省略するとデフォルトのビット長が指定される．なお，文字列を扱いたい場合はNumpyではなくリストかPandasを用いるのが良い．

x = np.array([1,2,3,4], dtype='int')
x

array([1, 2, 3, 4])

x = np.array([1,2,3,4], dtype='float')
x

array([1., 2., 3., 4.])

既存のNumPy配列に対してデータ型を変更したい場合はastypeメソッドを用いる．

# データ型を整数に変更
x = x.astype(int)
x.dtype

dtype('int64')

3.1.5. NumPy配列の属性

NumPy配列の形状や要素数などを属性と呼ぶ． NumPy配列は以下のような属性を持つ：

• shape：配列の形状

• ndim：配列の次元数

• size：配列の全要素数

• dtype：配列のデータ型

配列xに対してx.shapeなどとすると，対応する属性を取得することができる．

# 配列の作成
x1 = np.array([1,2,3,4,5,6])
print(x1)
x2 = np.array([[1,2,3], [4,5,6], [7,8,9]]).astype(float)
print(x2)

[1 2 3 4 5 6]
[[1. 2. 3.]
 [4. 5. 6.]
 [7. 8. 9.]]

# 配列の形状
print(x1.shape)
print(x2.shape)

(6,)
(3, 3)

# 次元数
print(x1.ndim)  # 1次元
print(x2.ndim)  # 2次元

1
2

# 配列の全要素数
print(x1.size)
print(x2.size)

6
9

# 配列のデータ型
print(x1.dtype)
print(x2.dtype)

int64
float64

3.1.6. 演習問題

• np.array関数を用いて様々なデータ型の配列を作成せよ

• 作成した配列について，いくつかの属性を取得せよ

• astypeメソッドを用いて，作成した配列のデータ型を変更せよ

• dtypeメソッドを用いて，変更した配列のデータ型を確認せよ

3.2. ベクトルと行列について

データ分析をする上でベクトルと行列の演算（つまり線形代数）は避けて通ることができない．実は，NumPyはベクトルや行列を扱うためのパッケージといっても過言ではない．以下，ベクトルと行列について簡単に説明する．

3.2.1. ベクトル

以下のように数字を1方向に並べたものをベクトルと呼ぶ：

\[\begin{split} \left( \begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right),\hspace{0.5cm} (1, 2, 3, 4) \end{split}\]

１つ目は数字が縦に並んでいるので縦ベクトル，２つ目は横ベクトルと呼ぶ．

ベクトルを構成する各要素を成分と呼ぶ．例えば，上の縦ベクトルは第0成分が1，第1成分が2，第2成分が3である．NumPyでは，横ベクトルは1次元のNumPy配列，縦ベクトルは2次元のNumPy配列によって以下のように実現できる：

np.array([1,2,3])

array([1, 2, 3])

np.array([[1], [2], [3]])

array([[1],
       [2],
       [3]])

\((a_{1}, a_{2})\)というベクトルは，\(xy\)平面上の任意の点から\(x\)方向に\(a_{1}\)，\(y\)方向に\(a_{2}\)進んだ点まで引いた矢印によって可視化できる．つまり，ベクトルというのは向きと長さ（大きさ）を持った量である．ベクトルの大きさは矢印の始点から終点までの距離に対応するので

\[ \sqrt{a_{1}^{2} + a_{2}^{2}} \]

と表される． スポーツデータの分析では，選手の速度を求めることがよくあるが，速度というのは向きと大きさを持つ量であるので，速度ベクトルとして表すことができる．

3.2.2. 行列

ベクトルは数字を一方向に並べたものであったが，以下のように数字を縦と横に並べたものを考える：

\[\begin{split} \left( \begin{array}{ccc} 3 & 5 & 7 \\ 1 & 0 & 9 \\ 2 & 4 & 3 \end{array} \right) \end{split}\]

これを行列と呼ぶ．

行列はベクトルを並べたものと捉えることもできる． 上の行列を横方向に切ると，以下のように３つのベクトルに分割することができる：

\[ \left( \begin{array}{c} 3 & 5 & 7 \end{array} \right), \left( \begin{array}{c} 1 & 0 & 9 \end{array} \right), \left( \begin{array}{c} 2 & 4 & 3 \end{array} \right) \]

これらを行と呼び，それぞれを0から始まる行番号によって0行，1行，2行などという． NumPyおよびPandasでは，行番号が増減する軸をaxis=0と表す．

一方，行列を縦方向に切ると

\[\begin{split} \left( \begin{array}{ccc} 3 \\ 1 \\ 2 \end{array} \right),\hspace{0.5cm} \left( \begin{array}{ccc} 5 \\ 0 \\ 4 \end{array} \right)\hspace{0.5cm} \left( \begin{array}{ccc} 7 \\ 9 \\ 3 \end{array} \right) \end{split}\]

に分割することができる． これを列と呼び，0から始まる列番号によって0列，1列，2列などという． NumPyおよびPandasでは，列番号が増減する軸をaxis=1と表す．

行列の形状は行数と列数の組み合わせで \( 3\times 3 \) 行列などと表す（1つ目の3は行数，2つ目の3は列数）．また，行列の成分は行番号 \( i \) と列番号 \( j \) を用いて \( (i, j) \) 成分などと表す．例えば，上の行列の \((0, 1)\) 成分は2である．

行列は2次元のNumPy配列によって以下のように実現できる：

np.array([[3, 5, 7], [1, 0, 9], [2, 4, 3]])

array([[3, 5, 7],
       [1, 0, 9],
       [2, 4, 3]])

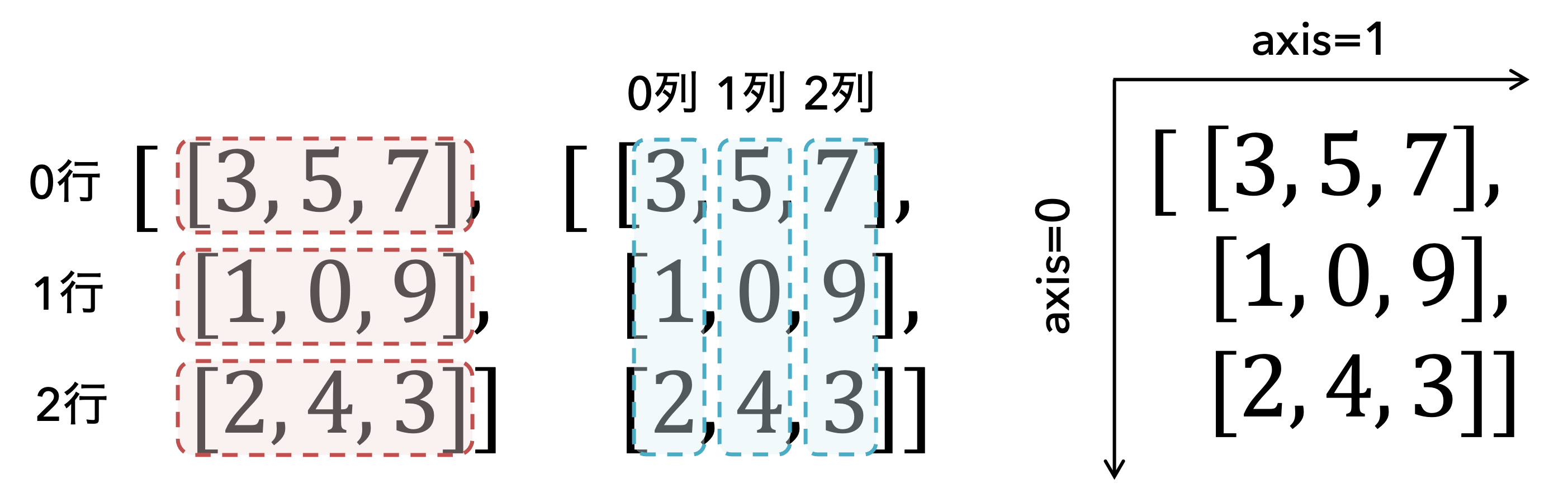
図 3.1 行列の例

3.3. NumPy配列の生成

NumPy配列を生成するには，主にリストを変換する方法と配列生成関数を使う方法がある．

3.3.1. リストを変換する

リストからNumPy配列を作るには，np.array関数を用いる

np.array([1,2,3,4])

array([1, 2, 3, 4])

# 3x2行列
np.array([[1,2], [3, 4], [5, 6]])

array([[1, 2],
       [3, 4],
       [5, 6]])

もし，各要素の型が一致しない場合，以下のように自動的に型が統一される

np.array([1, 2.0, 3])

array([1., 2., 3.])

3.3.2. 配列生成関数を使う

予めリストが与えられている場合や配列の要素が分かっていてサイズが小さい場合には上の方法で問題ないが，それ以外の場合にはNumPyの配列生成関数を利用するのが良い．

等間隔の数列を作成する

まず，等間隔の数列を作る関数として，np.arange()とnp.linspace()がある．

• np.arange(start, end, step)

  • start以上end未満の範囲でstep間隔の数列を生成する．

• np.linspace(start, end, num)

  • startからendの間をnum等分した数列を生成する．

この２つはNumPyの関数の中でも特に多用するので覚えておいた方が良い．

# 0以上20未満の範囲で2ずつ増加する数列
np.arange(0, 20, 2)

array([ 0,  2,  4,  6,  8, 10, 12, 14, 16, 18])

# endだけを指定する
np.arange(10)

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# 0から1までを5分割した数列
np.linspace(0, 1, 5)

array([0.  , 0.25, 0.5 , 0.75, 1.  ])

規則的な配列を生成する

以下のように，規則的な配列（全ての要素が同じ値であるなど）を生成する関数も用意されている：

• np.zeros(shape)

  • 全ての要素が0のshape形状の配列を生成する．

• np.ones(shape)

  • 全ての要素が1のshape形状の配列を生成する．

• np.full(shape, fill_value)

  • 全ての要素がfill_valueのshape形状の配列を生成する．

# 要素が全て0である長さ10の整数配列
np.zeros(10, dtype=int)

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])

# 要素が全て1である3行5列の浮動小数点数配列
np.ones([3, 5], dtype=float)

array([[1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1.]])

# 要素がすべて100である3x5配列
np.full([3, 5], 100)

array([[100, 100, 100, 100, 100],
       [100, 100, 100, 100, 100],
       [100, 100, 100, 100, 100]])

以上の関数について，既存の配列xと同じ形状にしたい場合はnp.zeros_like(x), np.ones_like(x), np.full_like(x)を用いる．

x = np.array([[1, 2, 3], [4, 5, 6]])

np.zeros_like(x)

array([[0, 0, 0],
       [0, 0, 0]])

np.ones_like(x)

array([[1, 1, 1],
       [1, 1, 1]])

np.full_like(x, 5)

array([[5, 5, 5],
       [5, 5, 5]])

ランダムな配列（乱数）

ランダムな値（乱数）を生成する関数も用意される．以下に一例を示す．

# 0以上1未満の一様実数乱数を要素とする3x4配列
np.random.random_sample([3, 4])

array([[0.421, 0.182, 0.227, 0.842],
       [0.315, 0.002, 0.506, 0.941],
       [0.54 , 0.115, 0.372, 0.097]])

# 10以上20未満の一様整数乱数を要素とする3x4配列
np.random.randint(10, 20, [3, 4])

array([[14, 10, 12, 15],
       [11, 12, 11, 14],
       [12, 13, 17, 10]])

# 平均5，標準偏差0.5の正規乱数を要素とする3x4配列
np.random.normal(5, 0.5, [3, 4])

array([[4.088, 5.3  , 4.997, 4.785],
       [5.193, 4.897, 3.747, 5.182],
       [5.211, 4.581, 6.032, 5.542]])

もし，乱数を生成する際にシードを指定したい場合はnp.random.seed関数を用いる． np.random.seed(seed=10)のようにシード値を指定することで，再現性のある乱数を生成することができる（何度実行しても同じ乱数が生成される）．

np.random.seed(seed=10)
np.random.randint(0, 100, 10)

array([ 9, 15, 64, 28, 89, 93, 29,  8, 73,  0])

3.3.3. 演習問題

以下の配列を生成せよ：

# 0から100まで2ずつ増加する数列
[0, 2, 4, ..., 96, 98, 100]

# NumPyを使わずに

# NumPyを使って

# 作成した配列の要素数を取得

以下の配列を生成せよ：

# 要素が全て5である3x4配列
[[5, 5, 5, 5],
 [5, 5, 5, 5],
 [5, 5, 5, 5]]

# NumPyを使わずに

# NumPyを使って

# 作成した配列の形状を取得

以下の配列をNumPyを使って生成せよ

# -1以上1未満の範囲で0.1ずつ増加する配列

# 10から2まで2ずつ減少する配列

# 0から10までを3分割した配列

# 要素が全て0である5x1の浮動小数配列

# 要素が全て1である2x7の整数配列

# 要素が全て0.5である長さ10の1次元配列

以下の配列xと同じ形状の配列を生成せよ

np.random.seed(seed=5)
x = np.random.rand(15, 7)
print(x)

[[0.222 0.871 0.207 0.919 0.488 0.612 0.766]
 [0.518 0.297 0.188 0.081 0.738 0.441 0.158]
 [0.88  0.274 0.414 0.296 0.629 0.58  0.6  ]
 [0.266 0.285 0.254 0.328 0.144 0.166 0.964]
 [0.96  0.188 0.024 0.205 0.7   0.78  0.023]
 [0.578 0.002 0.515 0.64  0.986 0.259 0.802]
 [0.87  0.923 0.002 0.469 0.981 0.399 0.814]
 [0.546 0.771 0.485 0.029 0.087 0.111 0.251]
 [0.965 0.632 0.817 0.566 0.635 0.812 0.927]
 [0.913 0.825 0.094 0.361 0.036 0.546 0.796]
 [0.051 0.189 0.365 0.244 0.795 0.352 0.639]
 [0.493 0.583 0.939 0.944 0.112 0.844 0.346]
 [0.101 0.383 0.51  0.961 0.372 0.012 0.86 ]
 [0.111 0.478 0.85  0.515 0.447 0.8   0.02 ]
 [0.573 0.411 0.985 0.801 0.054 0.19  0.452]]

# xの形状を取得

# xのデータ型を取得

# xと同じ形状で全ての要素が0

# xと同じ形状で全ての要素が1

# xと同じ形状で全ての要素が3

3.4. NumPy配列の操作

3.4.1. 配列のインデックス参照

配列中の要素が先頭から何番目かを表す番号をインデックスと呼ぶ． 1次元配列は1つのインデックス，2次元配列は2つのインデックス（行番号と列番号に対応するインデックス）によって指定する． Pythonではインデックスが0から始まることに注意する．

インデックスを用いて配列の一部分を取り出すことをインデックス参照と呼ぶ． NumPy配列に対するインデックス参照の方法はリストと同様であり，必要なインデックスを角カッコ[]で指定することで \(i\) 番目要素にアクセスできる．

1次元配列の場合

x1 = np.array([1,2,3,4,5,6])
x1

array([1, 2, 3, 4, 5, 6])

# 0番目要素
x1[0]

1

# 4番目要素
x1[4]

5

配列の末尾から \( i \) 番目の要素にアクセスするには負のインデックスを用いる．

# 末尾の要素
x1[-1]

6

2次元配列の場合

2次元配列では，カンマで区切ってarr[0, 0]のようにアクセスする． 行番号→列番号の順番で指定する．

※ arr[0][0]のように指定することもできるが非推奨．

x2 = np.array([[1,2,3], [4,5,6]]).astype(float)
x2

array([[1., 2., 3.],
       [4., 5., 6.]])

# (0, 1)要素
x2[0, 1]

2.000

# (1, 0)要素
x2[1, 0]

4.000

複数要素の参照（ファンシーインデックス参照）

インデックス参照の際にインデックスをリストにすることで，複数の要素をまとめて参照することができる． これをファンシーインデックス参照と呼ぶ． 詳しくは付録を参照のこと：ファンシーインデックス参照

x1 = np.random.randint(100, size=10)
x1

array([73, 27, 80, 69, 72, 44, 75,  2,  9,  3])

# 3, 4, 7番目の要素
x1[[3, 4, 7]]

array([69, 72,  2])

x2 = np.random.randint(100, size=(5, 5))
x2

array([[92, 70, 73, 37, 77],
       [10, 64, 60, 63, 17],
       [21, 97,  7, 48, 46],
       [29, 91, 18, 60, 66],
       [56, 27,  4, 38, 55]])

# 第0行と第2行
x2[[0, 2]]

array([[92, 70, 73, 37, 77],
       [21, 97,  7, 48, 46]])

3.4.2. 配列のスライス

配列中の連続する要素を取り出す操作をスライスと呼ぶ． NumPyでは，以下のようなコロン:を用いた表記により配列の連続する要素を取り出すことができる：

x[i_start: i_end: step]

ここで，i_startは始めのインデックス，i_endは終わりのインデックス，stepは間隔を表す． i_start，i_end，stepのいずれかが指定されていない場合はデフォルト値として，i_start=0，i_end=その次元のsize，step=1が指定される． 通常はstepを省略する．

1次元配列のスライス

x = np.arange(10)
x

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# インデックスが0以上5未満の要素
x[0:5]

array([0, 1, 2, 3, 4])

# インデックスが0以上5未満の要素（startの省略）
x[:5]

array([0, 1, 2, 3, 4])

# インデックスが5以上の要素（endの省略）
x[5:]

array([5, 6, 7, 8, 9])

# 先頭から1つおき（startとendの省略）
x[::2]

array([0, 2, 4, 6, 8])

# インデックス1からスタートして1つおき（endの省略）
x[1::2]

array([1, 3, 5, 7, 9])

stepが負の場合，i_startとi_endのデフォルト値が入れ替わるので，配列を逆順にすることができる．

# 逆順にすべての要素
x[::-1]

array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])

2次元配列のスライス

2次元配列の場合は，行番号と列番号をカンマで区切って指定する．

x2 = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12], [13, 14, 15]])
x2

array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12],
       [13, 14, 15]])

# 0~1行かつ0~1列
x2[0:2, 0:2]

array([[1, 2],
       [4, 5]])

行の抽出

2次元配列で行を抽出する場合には単に行番号を指定するだけで良い．

# 第1行
x2[0]

array([1, 2, 3])

# 1行おき
x2[0::2]

array([[ 1,  2,  3],
       [ 7,  8,  9],
       [13, 14, 15]])

# 1行目以降
x2[1:]

array([[ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12],
       [13, 14, 15]])

列の抽出

2次元配列で列を抽出する場合には，行方向にはコロン：を指定し，列方向に抽出したい列番号を指定する．

# 第0列
x2[:, 0]

array([ 1,  4,  7, 10, 13])

# 1列目以降
x2[:, 1:]

array([[ 2,  3],
       [ 5,  6],
       [ 8,  9],
       [11, 12],
       [14, 15]])

3.4.3. 配列への代入

インデックス参照やスライスによって抽出した配列要素に代入すると，元の配列が変更される． この機能を用いると，NumPy配列の一部分を変更することができる．

1次元の場合

x1 = np.arange(10)
x1

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# 2番目要素を-2に変更
x1[2] = -2
x1

array([ 0,  1, -2,  3,  4,  5,  6,  7,  8,  9])

# 0~4番目要素までを-1に変更
x1[0:5] = -1
x1

array([-1, -1, -1, -1, -1,  5,  6,  7,  8,  9])

2次元の場合

x2 = np.array([[1,2,3], [4,5,6], [7,8,9]])
x2

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

# (0,0)成分を12に変更
x2[0, 0] = 12
x2

array([[12,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9]])

# 第1行を[-4, -5, -6]に変更
x2[1] = [-4, -5, -6]
x2

array([[12,  2,  3],
       [-4, -5, -6],
       [ 7,  8,  9]])

# 第2列を[10, 20, 30]に変更
x2[:, 2] = [10, 20, 30]
x2

array([[12,  2, 10],
       [-4, -5, 20],
       [ 7,  8, 30]])

3.4.4. 演習問題

以下の配列xに対し，インデックス参照とスライスを用いて指定された１部分を抽出せよ．

np.random.seed(seed=10)
x = np.random.randint(0, 100, [5, 10])
x

array([[ 9, 15, 64, 28, 89, 93, 29,  8, 73,  0],
       [40, 36, 16, 11, 54, 88, 62, 33, 72, 78],
       [49, 51, 54, 77, 69, 13, 25, 13, 92, 86],
       [30, 30, 89, 12, 65, 31, 57, 36, 27, 18],
       [93, 77, 22, 23, 94, 11, 28, 74, 88,  9]])

# (3,7)成分

# 第1行

# 第5列

# 0~2行かつ5列以降

配列への代入によって以下の配列を作成せよ

# 中央だけ0
array([[1., 1., 1.],
       [1., 0., 1.],
       [1., 1., 1.]])

# 第2行だけ連番
array([[0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.],
       [1., 2., 3., 4., 5.]])

# 第1列だけ-1で後は10
array([[10, -1, 10],
       [10, -1, 10],
       [10, -1, 10],
       [10, -1, 10],
       [10, -1, 10]])

以下の配列xを基に指定された配列を作成せよ

x = np.arange(0, 25).reshape(5, 5)
x

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19],
       [20, 21, 22, 23, 24]])

# 真ん中だけ抽出
array([[ 6,  7,  8],
       [11, 12, 13],
       [16, 17, 18]])

# 逆順
array([[24, 23, 22, 21, 20],
       [19, 18, 17, 16, 15],
       [14, 13, 12, 11, 10],
       [ 9,  8,  7,  6,  5],
       [ 4,  3,  2,  1,  0]])

3.5. 条件付き抽出

3.5.1. ブールインデックス参照

ブールインデックス参照とは？

次のような任意の配列を考える．

x1 = np.random.randint(0, 100, 5)
x1

array([15, 18, 80, 71, 88])

この配列と同じ形状で各要素がTrueまたはFalseである以下のような配列を用意する：

index_bool = np.array([False, True, False, True, False])
index_bool

array([False,  True, False,  True, False])

このような配列をブールインデックス配列と呼び，そのデータ型はbool型である． 元の配列x1に対して，ブールインデックスを用いて参照すると，Trueの要素だけを抽出することができる．これをブールインデックス参照と呼ぶ．

# Trueの要素だけ抽出
x1[index_bool]

array([18, 71])

ブールインデックス参照による条件付き抽出

ブールインデックスは比較演算子<, >, ==, !=, %などを用いて元の配列から自動的に取得することができる． 例えば，配列x1の中で値が50未満の要素だけ抽出したい場合には以下のようにする：

x1 = np.random.randint(0, 100, 20)
x1

array([11, 17, 46,  7, 75, 28, 33, 84, 96, 88, 44,  5,  4, 71, 88, 88, 50,
       54, 34, 15])

# ブールインデックスの取得
x_bool = (x1 < 50)
x_bool

array([ True,  True,  True,  True, False,  True,  True, False, False,
       False,  True,  True,  True, False, False, False, False, False,
        True,  True])

# 50未満の要素の抽出
x1[x_bool]

array([11, 17, 46,  7, 28, 33, 44,  5,  4, 34, 15])

# 50未満の要素の抽出（条件を直接指定）
x1[x1 < 50]

array([11, 17, 46,  7, 28, 33, 44,  5,  4, 34, 15])

ブールインデックス参照は多次元配列でも同様の方法で実現できる． また，比較演算子を変えれば，以下のように様々な条件で要素を抽出することができる．

x2 = np.arange(35).reshape(5, 7)
x2

array([[ 0,  1,  2,  3,  4,  5,  6],
       [ 7,  8,  9, 10, 11, 12, 13],
       [14, 15, 16, 17, 18, 19, 20],
       [21, 22, 23, 24, 25, 26, 27],
       [28, 29, 30, 31, 32, 33, 34]])

# 10未満
x2[x2 < 10]

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# 10以上
x2[x2 >= 10]

array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,
       27, 28, 29, 30, 31, 32, 33, 34])

# 2に等しくない
x2[x2 != 2]

array([ 0,  1,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17,
       18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34])

# 2に等しい
x2[x2 == 2]

array([2])

# 2で割り切れる
x2[x2 % 2 == 0]

array([ 0,  2,  4,  6,  8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32,
       34])

以下のように複数の条件を指定することもできる．ただし，各条件は括弧()で囲む．

# 1より大きくかつ5未満の要素
x2_bool = (x2 > 1) & (x2 < 5)
x2_bool

array([[False, False,  True,  True,  True, False, False],
       [False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False]])

x2[x2_bool]

array([2, 3, 4])

# 1または5
x2[(x2 == 1) | (x2 == 5)]

array([1, 5])

ブールインデックス参照による代入

ブールインデックス参照による条件抽出と代入を組み合わせれば，配列の中で条件を満たす要素だけ値を変更することができる．

x1 = np.arange(-5, 10, 1)
x1

array([-5, -4, -3, -2, -1,  0,  1,  2,  3,  4,  5,  6,  7,  8,  9])

# 負の値を持つ要素を0に変更
x1[x1 < 0] = 0
x1

array([0, 0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# 2で割り切れる要素を2倍
x1[x1 % 2==0] *= 2
x1

array([ 0,  0,  0,  0,  0,  0,  1,  4,  3,  8,  5, 12,  7, 16,  9])

x2 = np.arange(9).reshape(3, 3)
x2

array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

# 4以上の要素を10に変更
x2[x2 >= 4] = 10
x2

array([[ 0,  1,  2],
       [ 3, 10, 10],
       [10, 10, 10]])

3.5.2. 演習問題

以下の配列xから指定した条件を満たす要素を抽出せよ

np.random.seed(seed=5)
x = np.random.randint(-100, 100, 100)
x

array([  -1,   89,   18,   44,  -27,  -92,   90,   55,   12,   58,  -93,
         43,   13,   81,  -20,  -73,  -56,  -35,   75,  -70,  -14,   25,
         46,   21,   37,    6,  -59,   90,   29,    3,   44,  -95,  -42,
       -100,   32,   10,   64,    5,   79,  -73,  -69,  -98,  -32,  -62,
          5,   47,  -82,   13,   35,    0,    8,    9,   58,   90,  -89,
        -33,   24,   93,   83,   31,   -9,  -22,   55,   57,  -67,  -15,
         35,  -84,   -6,  -86,  -69,  -91,  -62,  -53,   44,   33,   62,
         73,   87,   52,   41,   18,  -69,  -68,  -24,   72,   33,   42,
         75,   -6,  -18,   28,   35,  -84,  -36,  -92,  -56,   26,   65,
         -6])

# 負の値を持つ要素

# 3の倍数

# 10以上50未満

# 10以下または50以上

以下の配列xから指定された配列を作成せよ．

np.random.seed(seed=30)
x = np.random.randint(-10, 10, [5, 3])
x

array([[-5, -5,  3],
       [ 3,  2, -8],
       [ 7,  4, -7],
       [-1, -3, -9],
       [ 7,  3, -7]])

# 3を20に変更
array([[-5, -5, 20],
       [20,  2, -8],
       [ 7,  4, -7],
       [-1, -3, -9],
       [ 7, 20, -7]])

# 3と-5を0に変更
array([[ 0,  0,  0],
       [ 0,  2, -8],
       [ 7,  4, -7],
       [-1, -3, -9],
       [ 7,  0, -7]])

# 負の値を全て-1に変更
array([[-1, -1,  3],
       [ 3,  2, -1],
       [ 7,  4, -1],
       [-1, -1, -1],
       [ 7,  3, -1]])

# 負の値を全て正に変更
array([[5, 5, 3],
       [3, 2, 8],
       [7, 4, 7],
       [1, 3, 9],
       [7, 3, 7]])

3.6. 配列の形状変更

付録を参照のこと：配列の形状変更

3.7. NumPy配列の演算

3.7.1. ユニバーサル関数（ufunc）

NumPy配列の演算（加減乗除など）は，for文で実装すると非常に低速になってしまう．そこで，高速な演算が可能なユニバーサル関数が用意されている．これは，配列に対して１つの関数を実行するだけで，全ての要素に対して演算が行われる機能である．例えば，以下のように1000万個の数値が格納された1次元のNumPy配列があるとする．

np.random.seed(seed=7)
D = np.random.randint(0, 100, size=int(1e7))
D

array([47, 68, 25, ..., 80, 97, 13])

いま，この1000万個の数値に対して平均値を求めようと思ったとき，最も単純な方法は以下のようなfor文による実装である：

%%time
M = 0
for i in range(len(D)):
    M += D[i]
    
print(M / len(D))

49.4999793
CPU times: user 963 ms, sys: 4.57 ms, total: 967 ms
Wall time: 972 ms

実行結果を見ると，平均を求めるという単純な演算であるにも関わらず，数秒の時間がかかっている（実行時間はPCのスペックによって変動する）．これは，データ数が非常に大きいことが原因である．

一方，NumPyには平均値を求めるためのユニバーサル関数numpy.meanが用意されている．これを用いると，上のように配列の各要素にアクセスすることなく関数を1回実行するだけで平均値を求めることができる：

%%time
np.mean(D)

CPU times: user 6.05 ms, sys: 513 µs, total: 6.56 ms
Wall time: 5.92 ms

49.500

この場合の実行時間はfor文を用いた場合の1/100以下となっていることがわかる（実行時間はPCのスペックによって変動する）．

このように，NumPyのユニバーサル関数を使った演算は，配列のサイズが大きくなるにつれてfor文を用いた場合よりもずっと効率的になる．そこで，Pythonのプログラムでfor文を見つけたら，まずはNumPyのユニバーサル関数で置き換えられるかどうかを検討することが重要である．

3.7.2. 配列の演算規則

NumPy配列の演算規則は以下のようにまとめられる：

• NumPy配列と数値の演算では，配列の全ての要素に演算が適用される

• 同じ形状を持つ２つの配列の演算では，各配列の同じ要素同士で演算が行われる．

• 異なる形状を持つ配列の演算には特別な規則（ブロードキャスト）が適用される． ※ 詳しくは付録を参照のこと：ファンシーインデックス参照

配列と数値の演算

まず，配列と数値の演算は，配列の全ての要素に演算が適用される．

# 配列の生成
x2 = np.array([[1, 2, 3], [4, 5, 6]])
x2

array([[1, 2, 3],
       [4, 5, 6]])

# 足し算
x2 + 5

array([[ 6,  7,  8],
       [ 9, 10, 11]])

# 引き算
x2 - 5

array([[-4, -3, -2],
       [-1,  0,  1]])

# 掛け算
x2 * 2 

array([[ 2,  4,  6],
       [ 8, 10, 12]])

# 割り算
x2 / 2

array([[0.5, 1. , 1.5],
       [2. , 2.5, 3. ]])

# 累乗
x2 ** 2

array([[ 1,  4,  9],
       [16, 25, 36]])

# 余り
x2 % 2

array([[1, 0, 1],
       [0, 1, 0]])

# 加減乗除
2*(x2 + 5 - 2)/3

array([[2.667, 3.333, 4.   ],
       [4.667, 5.333, 6.   ]])

同じ形状を持つ配列間の演算

次に，同じ形状をもつ２つの配列の演算では，各配列の同じ要素同士で演算が行われる．

# 配列の生成
x2 = np.array([[1, 2, 3], [4, 5, 6]])
x2

array([[1, 2, 3],
       [4, 5, 6]])

# 同じ要素同士の足し算
x2 + x2

array([[ 2,  4,  6],
       [ 8, 10, 12]])

# 同じ要素同士の引き算
x2 - x2

array([[0, 0, 0],
       [0, 0, 0]])

# 同じ要素同士の掛け算
x2 * x2

array([[ 1,  4,  9],
       [16, 25, 36]])

# 同じ要素同士の割り算
x2 / x2

array([[1., 1., 1.],
       [1., 1., 1.]])

3.7.3. 様々なユニバーサル関数

並び替え（ソート）：np.sort

元の配列を変更せずにソートされた配列を得るにはnp.sort関数を使用する．

# 配列の生成
x1 = np.random.randint(0, 100, 10)
x1

array([92, 57, 73, 25, 50, 72, 68, 89, 98, 45])

np.sort(x1)

array([25, 45, 50, 57, 68, 72, 73, 89, 92, 98])

2次元配列の場合，axisを指定することで行ごとや列ごとのソートが実現できる．

# 配列の生成
x2 = np.random.randint(0, 10, [5, 3])
x2

array([[6, 9, 3],
       [8, 1, 1],
       [6, 1, 7],
       [2, 4, 0],
       [4, 5, 4]])

# 列ごとにソート
np.sort(x2, axis=0)

array([[2, 1, 0],
       [4, 1, 1],
       [6, 4, 3],
       [6, 5, 4],
       [8, 9, 7]])

# 行ごとにソート
np.sort(x2, axis=1)

array([[3, 6, 9],
       [1, 1, 8],
       [1, 6, 7],
       [0, 2, 4],
       [4, 4, 5]])

重複の削除：np.unique

# 配列の生成
x1 = np.random.randint(0, 10, 100)
x1

array([6, 2, 1, 5, 6, 8, 8, 8, 6, 0, 0, 9, 5, 5, 7, 1, 5, 5, 4, 1, 8, 3,
       2, 9, 0, 0, 0, 1, 9, 5, 6, 6, 5, 4, 2, 1, 3, 9, 2, 8, 6, 7, 2, 1,
       3, 0, 9, 3, 0, 6, 6, 5, 0, 6, 3, 1, 0, 6, 3, 2, 9, 2, 4, 2, 6, 7,
       4, 9, 8, 7, 8, 1, 2, 3, 6, 8, 9, 2, 0, 7, 0, 3, 1, 6, 8, 9, 0, 3,
       0, 5, 6, 4, 1, 1, 5, 7, 2, 7, 9, 7])

np.unique(x1)

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

絶対値：np.abs

# 配列の生成
x = np.array([-2, -1, 0, 1, 2])

np.abs(x)

array([2, 1, 0, 1, 2])

三角関数

# πの取得
np.pi

3.142

# 角度データの生成
theta = np.array([np.pi/6, np.pi/3, np.pi/2, np.pi])

# ラジアンから°への変換
np.degrees(theta)

array([ 30.,  60.,  90., 180.])

# sin
np.sin(theta)

array([0.5  , 0.866, 1.   , 0.   ])

# cos
np.cos(theta)

array([ 0.866,  0.5  ,  0.   , -1.   ])

# tan
np.tan(theta)

array([ 5.774e-01,  1.732e+00,  1.633e+16, -1.225e-16])

指数関数

x = np.array([1, 2, 3])

# 平方根
np.sqrt(x)

array([1.   , 1.414, 1.732])

# 2^x
np.power(2, x)

array([2, 4, 8])

# e^x
np.power(np.e, x)

array([ 2.718,  7.389, 20.086])

# e^x
np.exp(x)

array([ 2.718,  7.389, 20.086])

対数関数

# 底が2
x = np.array([2**2, 2**3, 2**4])
np.log2(x)

array([2., 3., 4.])

# 常用対数（底が10）
x = np.array([10**2, 10**3, 10**4])
np.log10(x)

array([2., 3., 4.])

# 自然対数（底がe）
x = np.exp([1, 2, 3])
np.log(x)

array([1., 2., 3.])

3.7.4. 配列の集計

NumPyには，配列から平均値などの統計量を求めるためのさまざまな集計関数が用意されている． なお，np.nansumのようにnanを付けると，欠損値（NaN値）を無視して計算を行うことができる．

関数名	説明
np.sum	要素の合計を計算する
np.prod	要素の積を計算する
np.mean	要素の平均値を計算する
np.std	要素の標準偏差を計算する
np.var	要素の分散を計算する
np.min	最小値を見つける
np.max	最大値を見つける
np.median	要素の中央値を計算する
np.percentile	パーセンタイルを計算する
np.any	いずれかの要素がTrueであるかを評価する
np.all	すべての要素がTrueであるかを評価する

１次元配列の場合

# 配列の生成
np.random.seed(seed=2)
x = np.random.randint(0, 100, 10000)
x

array([40, 15, 72, ..., 98, 45, 28])

# 合計
np.sum(x)

499124

# 最大値
np.max(x)

99

# 最小値
np.min(x)

0

# 中央値
np.median(x)

50.000

# 平均値
np.mean(x)

49.912

# 標準偏差
np.std(x)

28.726

# 標本分散（nで割る）
np.var(x, ddof=0)

825.185

# 不偏分散（n-1で割る）
np.var(x, ddof=1)

825.267

2次元の場合

2次元の場合はaxisを指定することで，行ごと（axis=0），列ごと（axis=1）の集計が実現できる．

# 配列の生成
np.random.seed(seed=1)
x2 = np.random.randint(0, 100, [5, 5])
x2

array([[37, 12, 72,  9, 75],
       [ 5, 79, 64, 16,  1],
       [76, 71,  6, 25, 50],
       [20, 18, 84, 11, 28],
       [29, 14, 50, 68, 87]])

# 行方向（列ごと）
np.max(x2, axis=0)

array([76, 79, 84, 68, 87])

# 列方向（行ごと）
np.max(x2, axis=1)

array([75, 79, 76, 84, 87])

3.8. ファイル入出力

3.8.1. ファイルへの出力

NumPy配列xをファイルに出力するにはnp.savetxt関数を用いる．

# 配列の生成
x = np.arange(25).reshape(5, 5)

# 配列をcsv形式で保存する
np.savetxt('./array_ex.csv', x, fmt='%d', delimiter=',')  # 相対パスを指定

np.savetxtにはフォーマットfmt，区切り文字delimiter，エンコーディングencodingなどを指定できる．

3.8.2. ファイルからの読み込み

データをNumPy配列に読み込むにはnp.loadtxt関数を用いる．

arr = np.loadtxt('./array_ex.csv', delimiter=',', dtype='float')  # 相対パスを指定
arr

array([[ 0.,  1.,  2.,  3.,  4.],
       [ 5.,  6.,  7.,  8.,  9.],
       [10., 11., 12., 13., 14.],
       [15., 16., 17., 18., 19.],
       [20., 21., 22., 23., 24.]])

np.loadtxtには引数として区切り文字delimiter，データ型dtype，エンコーディングencodingなどが指定できる．delimiterを省略するとデフォルト値のスペース' 'となる．

3.9. 章末問題

問題A

以下のように，母平均5，母標準偏差0.5の正規分布に従うデータから100個を抽出した．

# 配列の生成
np.random.seed(seed=45)
x = np.random.normal(5, 0.5, 100)
x

array([5.013, 5.13 , 4.802, 4.898, 4.364, 3.702, 5.145, 4.563, 5.197,
       5.468, 4.992, 5.13 , 4.263, 5.401, 4.125, 4.752, 4.496, 5.013,
       4.939, 4.227, 4.697, 4.303, 4.686, 5.166, 4.229, 5.835, 4.75 ,
       5.337, 6.124, 4.173, 4.763, 4.849, 4.534, 5.555, 4.905, 5.639,
       4.723, 5.177, 4.78 , 4.788, 5.114, 5.29 , 4.573, 4.579, 4.672,
       4.927, 4.294, 4.865, 5.565, 4.33 , 4.875, 5.882, 4.704, 4.546,
       5.136, 4.998, 5.427, 4.205, 5.028, 5.053, 4.955, 4.643, 5.102,
       5.602, 5.042, 5.082, 5.187, 4.887, 4.664, 5.157, 5.742, 5.326,
       4.884, 5.592, 5.46 , 5.608, 4.058, 5.111, 5.908, 5.871, 4.97 ,
       4.705, 4.589, 4.974, 4.957, 5.216, 4.902, 4.67 , 4.877, 4.895,
       4.747, 4.281, 4.898, 4.716, 4.826, 4.485, 5.293, 5.186, 3.796,
       5.482])

このデータに対し，np.mean関数とnp.std関数を用いて標本平均と標本標準偏差を求めると以下のようになった．

np.mean(x)

4.930

np.std(x)

0.465

• NumPyの関数を使わずにxの標本平均を求め，上の結果と一致することを確かめよ． ただし，データ \( x = (x_{1}, x_{2}, \ldots, x_{n}) \) に対して，標本平均 \( \bar{x} \) は以下で定義される：

\[ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_{i} = \frac{x_{1}+x_{2}+\cdots+x_{n}}{n} \]

• NumPyの関数を使わずにxの標本標準偏差を求め，上の結果と一致することを確かめよ． ただし，データ \( x = (x_{1}, x_{2}, \ldots, x_{n}) \) に対して，標本標準偏差 \( \bar{\sigma} \) は以下で定義される：

\[ \bar{\sigma} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_{i} - \bar{x})^2} = \sqrt{ \frac{(x_{1}-\bar{x})^2+(x_{2}-\bar{x})^2+\cdots+(x_{n}-\bar{x})^2}{n} } \]

問題B

次のcsvファイルをダウンロードし，カレントディレクトリに保存せよ：player_England.csv
このファイルには，2017年度にイングランド・プレミアリーグに所属していた選手の選手ID，身長，体重のデータが保存されている． ただし，身長の単位はcm，体重の単位はkgである．

※ 本データはPappalardoデータセットを加工したものである（詳細はPappalardoデータセットの詳細）．

まず，このファイルをNumPy配列Dに読み込む：

# csvファイルを読み込む
D = np.loadtxt('./player_England.csv', delimiter=',', dtype='int')
D

array([[  3319,    180,     76],
       [    -1,   1000,   1000],
       [  3560,    179,     72],
       ...,
       [357712,    183,     92],
       [386197,    175,     71],
       [412919,    190,     76]])

配列Dは第0列に選手ID，第1列に身長，第2列に体重が格納されている． 例えば，Dの第0行目を見ると，選手IDが3319で身長180cm，体重76kgであることが分かる． このデータに対し，以下の問いに答えよ．

• 選手IDが-1となっている要素はダミーデータである．Dからダミーデータを削除し，改めて配列Dとせよ．

# 解答欄

• データに含まれる選手数を調べよ．

# 解答欄

• 選手IDが703の選手の身長と体重を調べよ．
  ※ この選手は吉田麻也選手である．2017年時点の体重と現在の体重を比較してみよ．

# 解答欄

• 配列Dから選手ID，身長，体重のデータを抽出し，それぞれI, H, Wという配列に格納せよ．

I = 
H = 
W = 

• 以下の方法により，身長の最小値，最大値を求めよ

  • 配列Hを昇順（小→大）に並び替え，先頭と末尾の要素を抽出する

  • np.min関数，np.max関数を用いる

# Hを昇順に並び替えて先頭と末尾の要素を抽出

# np.min, np.maxを用いる

• 肥満度を表す指標としてBMIが知られている．BMIは身長と体重を用いて以下で定義される：

(3.1)\[\begin{align} \mathrm{BMI} = \frac{体重 [kg]}{(身長 [m])^2} \end{align}\]

• 身長の単位をcmからmに変換し，H2に格納せよ．

# Hの単位をcm -> m
H2 = 

• 配列WとH2からBMIを求め，BMIという配列に格納せよ．

# BMIを求める
BMI = 

• BMIが18.5未満の選手が１人いる．この選手のIDを調べよ．
  ※ この選手はRekeem Jordan Harper選手である．
  ※ 日本肥満学会の基準では，BMIが18.5未満の場合を痩せ型と定義している．

# BMIが18.5未満を抽出